The geometric Pentagon, a five-sided polygon, holds a unique place in the realm of geometry. Its distinct symmetries and properties have fascinated mathematicians, artists, and architects for centuries. In this article, we will delve into the characteristics of the geometric Pentagon, its various types, and its applications in both mathematics and real-world contexts.
What Is A Pentagon?
'Penta' means 'five,' and 'gon' means 'angle' in Greek; hence, the term 'pentagon' is taken from the Greek language. The standard definition of a pentagon is a 5-sided, 5-angled, 2-dimensional polygon. If it's a true pentagon, then its five sides are all the same length, and its internal angles add up to 108 degrees. The inner curves of an irregular pentagon may be any combination of measures up to 540 degrees.
A Journey Through The History Of The Geometric Pentagon
Let us discuss the history of a geometric pentagon.
Ancient Beginnings - Early Recognition Of The Pentagon
The concept of the Pentagon dates back to ancient civilizations, with early mathematical texts and architectural designs showcasing its presence. In ancient Greece, scholars like Pythagoras and Euclid explored the geometric properties of polygons, including the Pentagon. Their contributions laid the groundwork for a deeper understanding of this unique five-sided figure.
Pythagorean Insights - Mystical Significance Of The Pentagram
The Pythagoreans, an ancient Greek philosophical and mathematical school, attached mystical and symbolic significance to the Pentagon, particularly within the context of the pentagram.
They believed that the Pentagon and its associated pentagram held spiritual and mathematical secrets, contributing to their profound influence on ancient mathematics and philosophy.
Greek Mathematics - Euclidean Geometry And The Pentagon
Euclid, the renowned Greek mathematician, systematically studied the properties of polygons, including the Pentagon, in his seminal work "Elements."
Through Euclidean geometry, he established foundational principles that continue to shape modern geometry. Euclid's treatment of the Pentagon marked a significant milestone in the historical development of mathematical knowledge.
Renaissance Rediscovery - The Pentagonal Revival
During the Renaissance, the study of ancient Greek mathematics experienced a revival in Europe. Scholars like Leonardo da Vinci and Luca Pacioli delved into the geometric intricacies of the Pentagon, recognizing its significance in both art and mathematics. The Pentagon's aesthetic appeal and mathematical elegance found renewed appreciation during this period.
Pentagons In Islamic Geometry - Artistic Elegance And Mathematical Precision
Islamic scholars made substantial contributions to geometry, emphasizing the aesthetic and mathematical potential of geometric shapes, including the Pentagon. Intricate patterns and designs featuring pentagonal elements emerged in Islamic art and architecture, leaving a lasting legacy in the world of geometric aesthetics.
Modern Advancements - From Pentagon To Pentagon Building
In the modern era, the geometric Pentagon found a symbolic embodiment in the Pentagon building, the headquarters of the United States Department of Defense. The five-sided structure, completed in 1943, serves as a prominent architectural testament to the enduring influence and significance of the Pentagon as both a geometric form and a symbol of defense and security.
Properties Of A Geometric Pentagon
The geometric Pentagon possesses a set of properties that distinguish it from other polygons and make it an exciting subject of study in geometry. Here are some fundamental properties of a geometric pentagon.
Five Sides
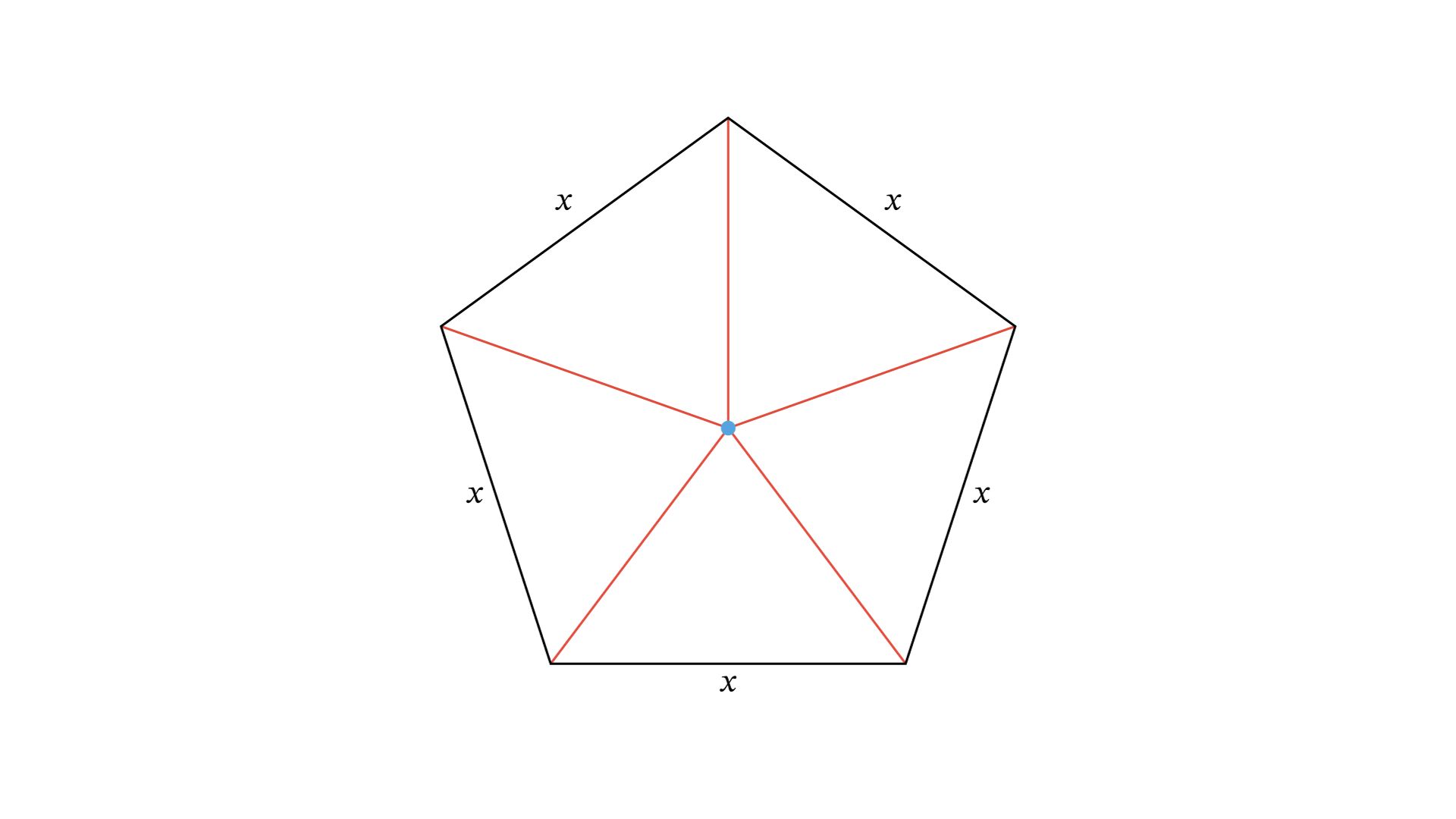
A geometric pentagon is defined as having precisely five sides. These sides connect five vertices.
The Sum Of Interior Angles
The sum of the interior angles in any pentagon is always 540 degrees. This property is a fundamental characteristic of pentagons and holds true for all types of pentagons.
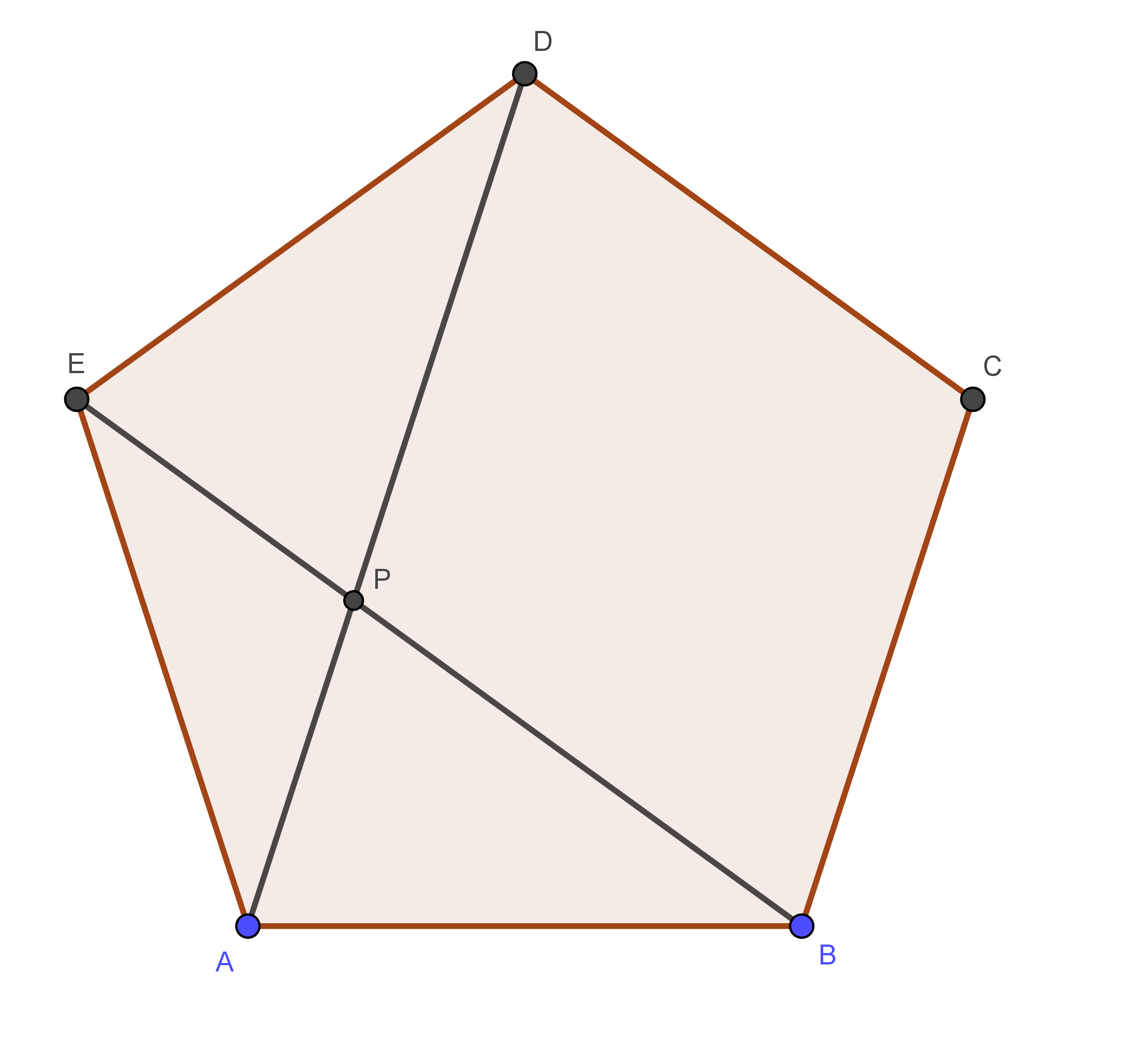
Diagonals
A geometric pentagon has five diagonals, which are line segments connecting non-adjacent vertices. The diagonals create interesting relationships within the Pentagon.
Symmetry
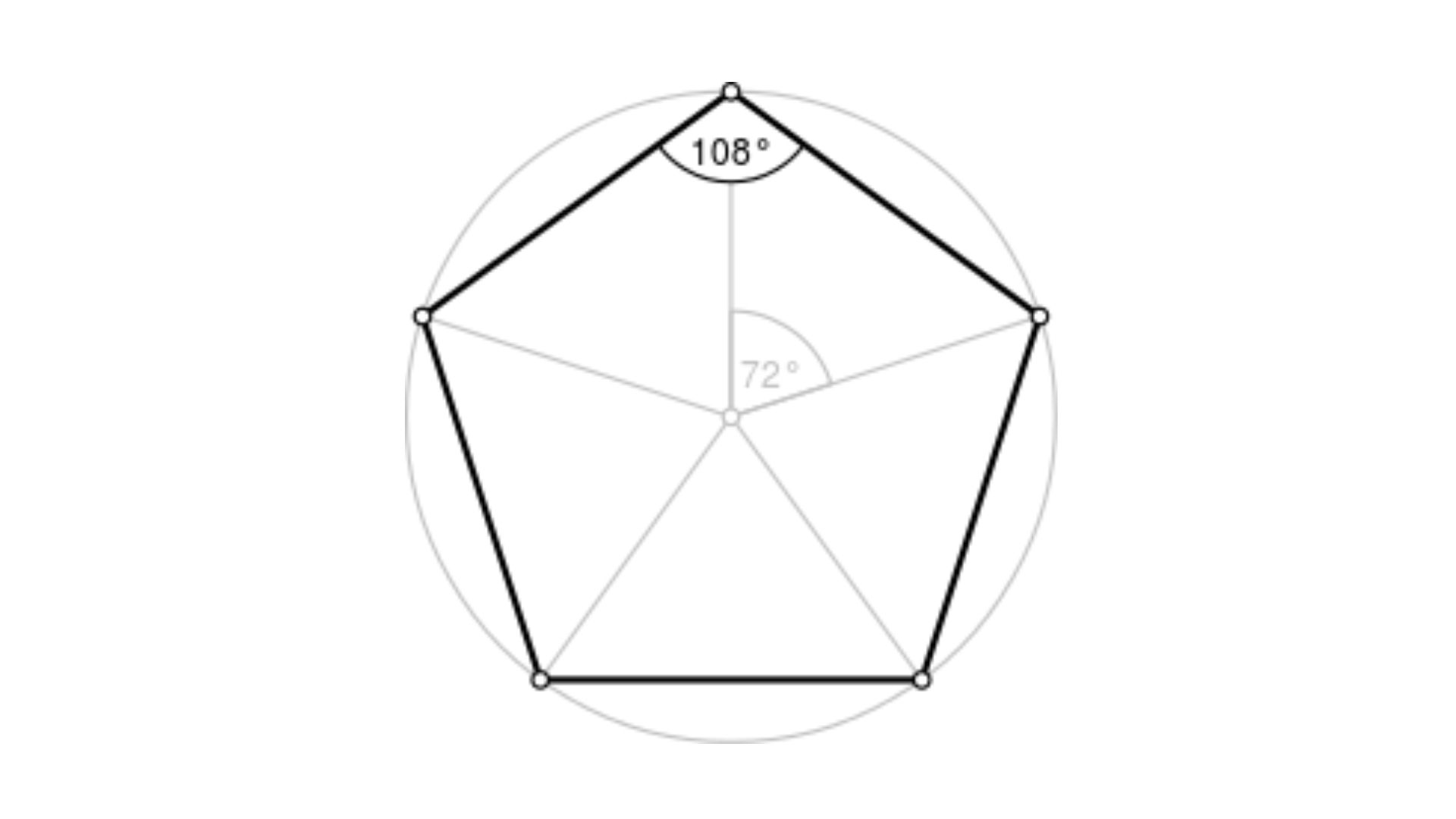
A regular pentagon has five lines of symmetry. Each line of symmetry divides the Pentagon into two congruent halves.
Exterior Angles
The exterior angles of a pentagon, formed by extending each side of the Pentagon outward, sum to 360 degrees. Each exterior grade corresponds to an interior angle of the Pentagon.
Angle Measures
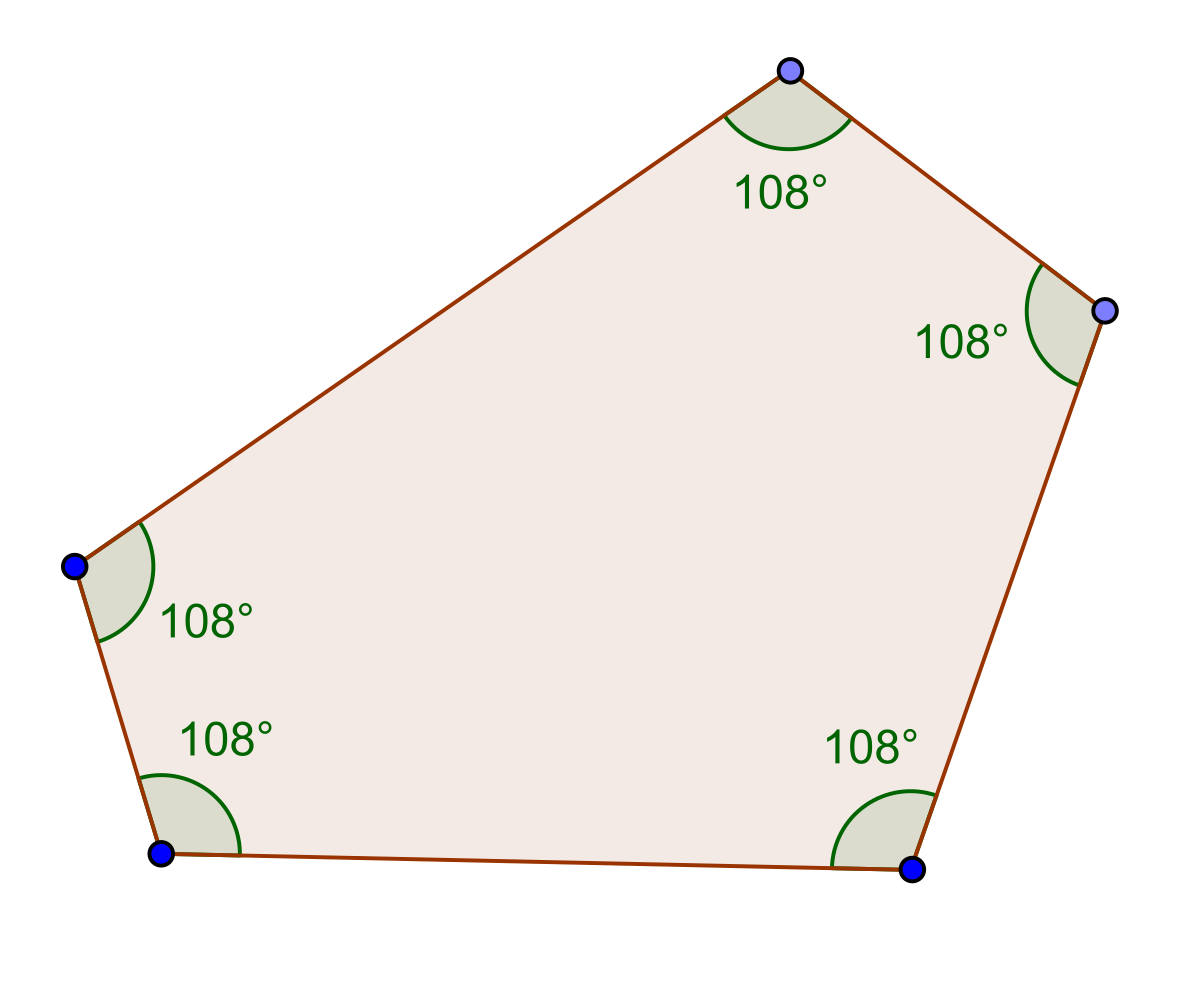
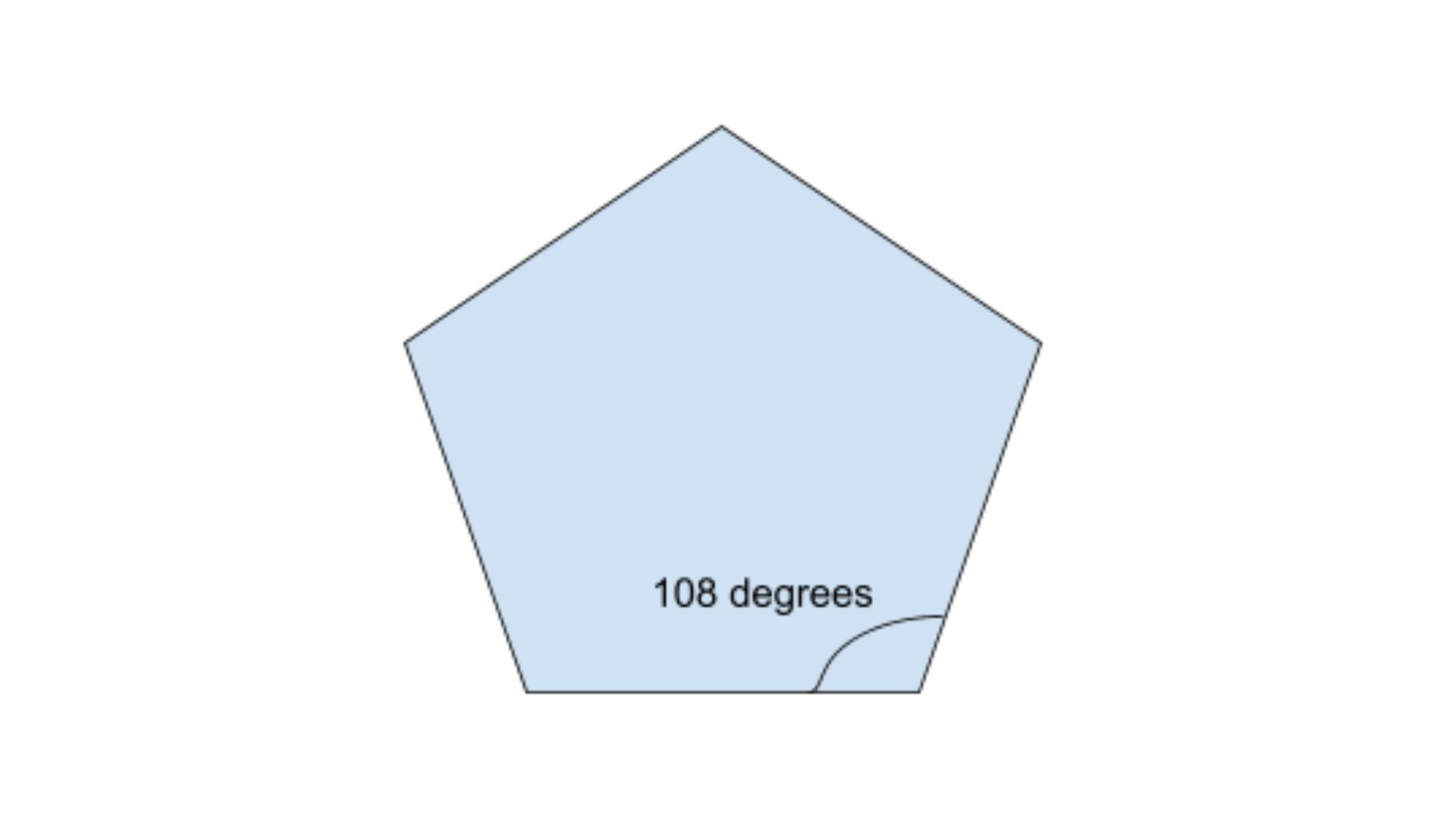
In a regular pentagon, all interior angles are of equal measure, each measuring 108 degrees. In irregular pentagons, the tips may vary.
Diagonal Lengths
The lengths of the diagonals in a geometric pentagon can vary depending on the type of Pentagon. In a regular pentagon, all diagonals are equal in size.
Golden Ratio
The ratio of the length of the longer diagonal to the shorter diagonal in a regular pentagon is very close to the golden ratio (Φ ≈ 1.618). This unique mathematical relationship is a source of fascination for mathematicians and artists.
Area
The area of a geometric pentagon can be calculated using different methods, such as dividing it into triangles or using trigonometric functions. The formula for the area may vary depending on the information available about the Pentagon.
Convex And Concave Forms
A pentagon can be convex, with all interior angles measuring less than 180 degrees, or concave, with at least one internal angle measuring more than 180 degrees.
Classification
Pentagons can be classified into various types, including regular, irregular, equilateral, equiangular, right, obtuse, acute, isosceles, and others, each with its own unique set of properties.
These properties make the geometric Pentagon a fascinating shape to study in mathematics and geometry. Its symmetry, angles, and relationships with other mathematical concepts contribute to its enduring significance in both theoretical and practical applications.
Types Of Geometric Pentagon
Geometric pentagons come in various forms, each with distinct characteristics. Here are the primary types of geometric pentagons:
Regular Pentagons
Regular pentagons have all sides of equal length and all interior angles measuring 108 degrees. They possess five lines of symmetry, resulting in a balanced and harmonious geometric figure.
Irregular Pentagons
Irregular pentagons have sides and angles of varying lengths and measures. Unlike regular pentagons, irregular ones lack uniformity, making them a diverse and interesting category of polygons.
Convex Pentagons
Convex pentagons have interior angles that are all less than 180 degrees. It means that no grade points inward, resulting in a polygon that "bulges out" rather than having any indentations.
Concave Pentagons
Concave pentagons have at least one interior angle greater than 180 degrees. They possess at least one angle that points inward, creating a "caved-in" appearance within the polygon.
Equilateral Pentagons
Equilateral pentagons have all sides of equal length, but not necessarily all angles are of equal measure. This combination of equal sides and varying angles creates a unique and intriguing polygon.
Equiangular Pentagons
Equiangular pentagons have all interior angles of equal measure, but not necessarily all sides are of equal length. This type of Pentagon prioritizes angle equality over side-length uniformity.
Right Pentagons
Right pentagons have one interior angle measuring precisely 90 degrees. This characteristic makes them particularly useful in specific mathematical contexts and constructions.
Obtuse Pentagons
Obtuse pentagons have at least one interior angle measuring more than 90 degrees. This property imparts a distinct angularity to the polygon, setting it apart from other types.
Acute Pentagons
Acute pentagons have all interior angles measuring less than 90 degrees. This characteristic lends the polygon a sharp and pointed appearance, reflecting its acute angles.
Isosceles Pentagons
Isosceles pentagons have at least two sides of equal length. However, not all angles are necessarily of equal measure, offering a balance of symmetry and variation within the polygon.
Geometric Pentagon Applications
The geometric Pentagon, with its unique properties and symmetries, finds applications in various fields. Here are some notable areas where the Pentagon is utilized.
Architecture And Design
Architects often incorporate pentagonal shapes and proportions in their designs to create aesthetically pleasing and structurally sound buildings. The Pentagon building in Washington, D.C., is a prime example of a pentagonal architectural design.
Tessellations
Pentagons play a crucial role in tessellations, which are repeating patterns formed by fitting shapes together without any gaps or overlaps. Artists and designers use pentagonal tessellations to create visually appealing patterns and artwork.
Engineering And Construction
The symmetries and proportions of the Pentagon can influence the design and layout of structural elements in engineering projects. The Pentagon's properties can contribute to the stability and integrity of construction.
Mathematical Research
Mathematicians study the properties of pentagons as part of broader geometric investigations. The relationships and symmetries inherent in pentagons can lead to insights in geometry and trigonometry.
Art And Sculpture
The Pentagon's unique form has long inspired artists. It serves as a foundational element in various art forms, influencing the composition of paintings, sculptures, and other visual creations.
Pentagonal Sports Fields
Some sports fields, such as soccer fields, are designed with a pentagonal shape. This design choice can have implications for the dynamics and strategy of the sport played on the field.
Pentagonal Prisms In 3D Geometry
Pentagons are central to the geometry of pentagonal prisms, three-dimensional figures with pentagonal bases and sides. These prisms have applications in architecture, engineering, and manufacturing.
Crystallography
In crystallography, the geometric properties of pentagons play a role in describing the structure of certain crystals. Understanding these geometric principles aids in the study of crystal lattice arrangements.
Pentagonal Paving Patterns
Pentagonal tiles or paving stones can be used in flooring and pavement designs. These patterns can add a distinctive and visually appealing touch to outdoor spaces.
Educational Tools
The Pentagon serves as a valuable educational tool for teaching geometry concepts. Its unique properties and symmetries make it a useful subject for hands-on learning and visual demonstrations.
Logo Design
Companies and organizations often use geometric shapes, including pentagons, in their logos. The balanced and structured nature of the Pentagon can convey stability and professionalism.
Interesting Facts About The Geometric Pentagon Shape
The pentagon shape, with its five sides, is a fascinating geometric figure that holds several intriguing facts. Here are some interesting facts about the Pentagon.
Ancient Mystique
The Pentagon has deep historical significance. Ancient cultures, including the Greeks and Egyptians, associated it with mystical and symbolic meanings, often attributing it to the concept of perfection and the divine.
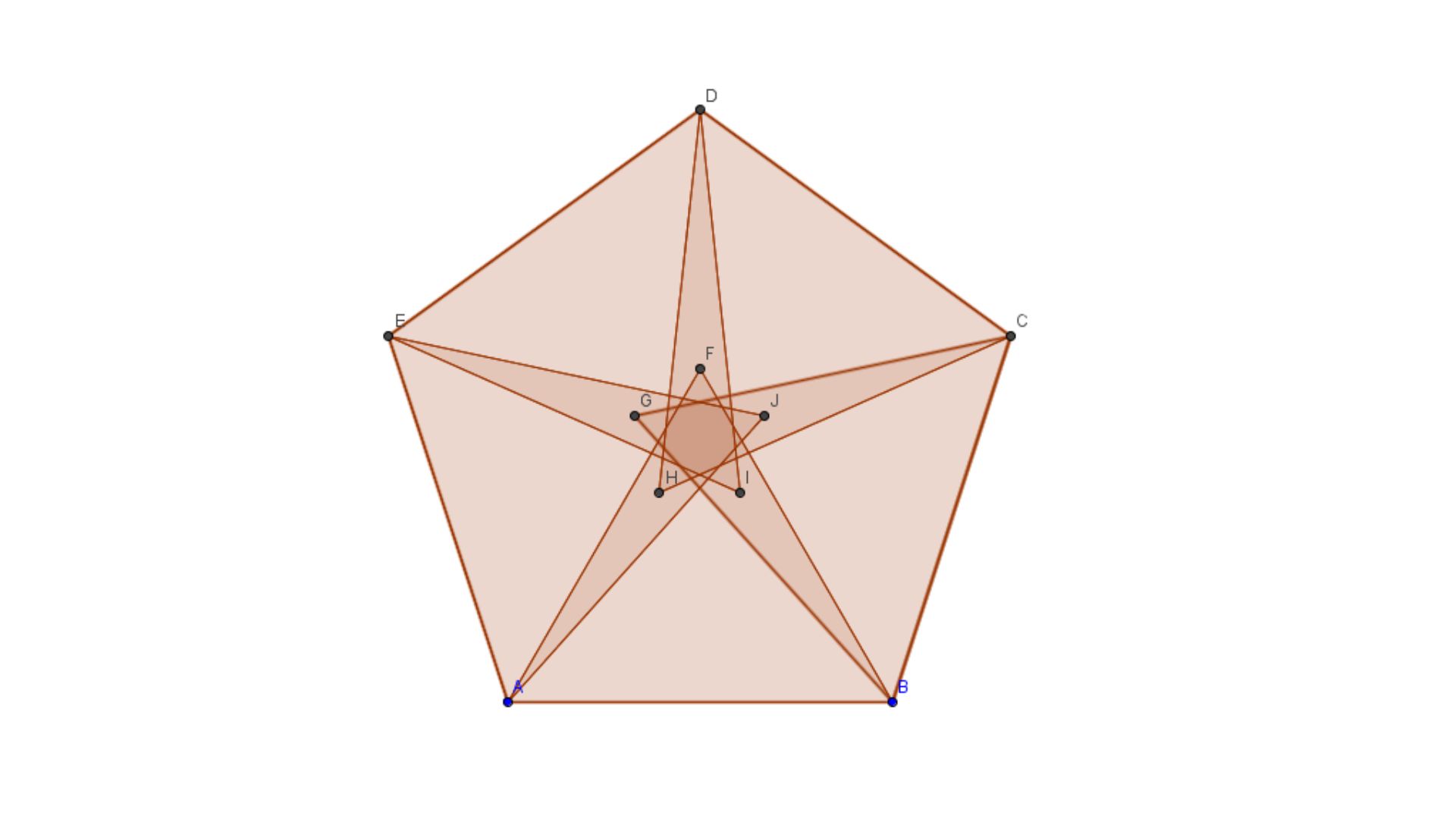
Mystical Pentagram
The Pentagon is closely linked with the pentagram, a five-pointed star. The Pythagoreans, an ancient Greek philosophical school, believed the Pentagon and pentagram held profound mathematical and spiritual secrets.
Golden Ratio Connection
In a regular pentagon, the ratio of the length of the longer diagonal to the shorter diagonal is approximately equal to the golden ratio (Φ ≈ 1.618). This mathematical relationship has captivated mathematicians and artists for centuries.
The Pentagon Building
The Pentagon, located in Arlington, Virginia, is one of the largest office buildings globally. It serves as the headquarters of the United States Department of Defense and is an iconic symbol of military power and defense.
Symmetry Marvel
A regular pentagon boasts five lines of symmetry, allowing it to be divided into five congruent triangles. This high level of balance sets the Pentagon apart from many other polygons.
Tessellation Challenge
Pentagons are among the few regular polygons that cannot tile a plane without gaps or overlaps by themselves. However, they can be combined with other shapes to create mesmerizing tessellations.
The Dürer Solid
In the early 16th century, the German artist and mathematician Albrecht Dürer discovered a unique solid with pentagonal faces. This solid, known as the "Dürer solid," has pentagonal faces that are not regular, adding to the intrigue surrounding the Pentagon.
Nature's Pentagons
Some star-shaped flowers, like the morning glory, exhibit pentagonal symmetry in the arrangement of their petals.
Crystallographic Marvels
Crystals can exhibit pentagonal symmetries in their structures. This phenomenon is central to the field of crystallography and contributes to our understanding of crystalline formations.
Architectural Influence
The Pentagon's unique shape has influenced the design of various structures and landmarks, including the United States Postal Service logo and the home plate in baseball.
Islamic Art And Geometry
Islamic art and architecture often feature intricate patterns and designs based on pentagonal geometry. It showcases the aesthetic appeal and mathematical elegance of the Pentagon.
Educational Utility
The Pentagon is commonly used as an educational tool to teach geometry concepts due to its easily recognizable form and symmetrical properties.
Geometric Pentagon Jewelries
Geometric pentagon jewelrytypically refers to jewelry designs that incorporate the shape of a pentagon, which is a five-sided polygon. These designs often emphasize clean lines, symmetry, and a modern aesthetic. Here are some ideas for geometric pentagon jewelry:
Pentagon Pendant Necklace
- Create a pendant featuring a pentagon-shaped charm.
- Experiment with materials like metal, wood, or acrylic for a modern touch.
- Add gemstonesor enamel for color accents.
Pentagon Earrings
- Design earringswith pentagon-shaped drops or studs.
- Consider using various materials such as silver, gold, or geometrically patterned fabric.
Pentagon Bracelet
- Craft a bracelet with pentagon-shaped links or charms.
- Connect the pentagons in an interlocking pattern for added interest.
Pentagon Ring
- Create a statement ringwith a pentagon-shaped setting for a gemstone.
- Opt for a minimalist design with a plain pentagon, or add intricate details for a more elaborate look.
Geometric Pentagon - FAQs
What Is Unique About The Pentagon Shape?
The Pentagon's internal angles total 540°. A regular pentagon has equal sides and angles. It's irregular otherwise. In the regular Pentagon, internal angles are 108° and outside angles 72°.
What Are The Three Characteristics Of A Pentagon?
Five congruent sides (equal length) and five congruent interior angles (108°) are required for a regular pentagon.
Are All Sides Of The Pentagon Equal?
In regular pentagons, all sides have identical lengths and angles. Equiangular forms have equal slopes. Since polygon internal angles total 360 degrees. Therefore, each stable Pentagon's interior tip is 108 degrees.
What Distinguishes A Regular Pentagon From An Irregular One?
A regular pentagon has all sides and angles equal, while an irregular pentagon has sides and angles of varying lengths and measures.
What Is The Sum Of Interior Angles In A Geometric Pentagon?
The sum of interior angles in a geometric pentagon is always 540 degrees.
Conclusion
The geometric Pentagon, with its intriguing properties and applications, remains an enduring symbol of symmetry and proportion. From its role in tessellations to its influence in architectural design, the Pentagon's presence is felt in various domains. Its allure continues to captivate mathematicians, artists, and architects alike, ensuring that it will remain a subject of fascination for generations to come.